What is Time Series?

What is Time Series?#

by Professor Throckmorton
for Time Series Econometrics
W&M ECON 408/PUBP 616
Slides

Definition#

  • A time series is a sequence of data points collected over time.

  • These data points are ordered by time, and the sequence of the data cannot be interchanged.

  • Time series analysis focuses on transforming, visualizing, and modeling this type of data.

  • When modeling a time series, its value at any time is random, i.e., the realization of a random variable.

  • Thus, a time series is a discrete stochastic process.

Plots#

  • A time series plot (or time plot) is a graph that visualizes the evolution of a time series.

    • Time, \(t\), is on the horizontal axis.

    • Observed values are on the vertical axis.

  • Time series plots are crucial for analysis, revealing patterns such as trend and seasonality.

  • The first step always is to plot the recorded data and do a visual examination, i.e., “eyeball econometrics.”

  • For economic time series data, usually we have observations at regular intervals, or frequencies, e.g., daily, monthly, quarterly, or annual.

Examples#

# Libraries
from fredapi import Fred
import pandas as pd
# Read Data
fred_api_key = pd.read_csv('fred_api_key.txt', header=None)
fred = Fred(api_key=fred_api_key.iloc[0,0])
data = fred.get_series('UNRATE').to_frame(name='UR')
print(data.head(2))
print(data.tail(2))

             UR
1948-01-01  3.4
1948-02-01  3.8
             UR
2025-06-01  4.1
2025-07-01  4.2

# Plotting
import matplotlib.pyplot as plt
# Plot
fig, ax = plt.subplots(figsize=(6.5,2.5));
ax.plot(data.UR);
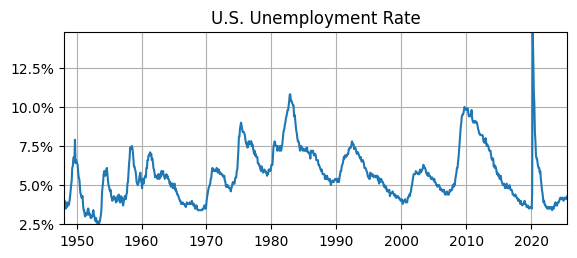
ax.set_title('U.S. Unemployment Rate');
ax.yaxis.set_major_formatter('{x:,.1f}%')
ax.grid(); ax.autoscale(tight=True)
_images/3758e90e41da87733f53cbefee8511afb8d187a214bb088e72ca80a40ee6b85c.png

Objectives#

  • Time series plots are useful for identifying

    • trends, i.e., long-term systematic patterns.

    • seasons, i.e., common patterns across years.

    • cycles, i.e, patterns related to economic recessions and expansions.

    • structural changes to trend, seasonal, or cyclical patterns.

    • outliers (anomalies).

  • Descriptive statistics are used to summarize the properties of time series, e.g., Mean/Expected Value, Variance/Std. Deviation, Autocorrelation, Skewness, Kurtosis, percentiles, and min/max are all useful descriptive statistics.

# Import libraries
#   Scientific computing, statistical functions
import scipy.stats as stats

# Mean
print(f'Most recent UR = {data.UR.iloc[-1]:.1f}%')
print(f'E(UR) = {stats.tmean(data.UR):.1f}%')
print(f'Std(UR) = {stats.tstd(data.UR):.1f}%')
print(f'Skew(UR) = {stats.skew(data.UR):.1f}')
print(f'Kurt(UR) = {stats.kurtosis(data.UR):.1f}')
print(f'min(UR) = {data.UR.min():.1f}%')
print(f'max(UR) = {data.UR.max():.1f}%')

Most recent UR = 4.2%
E(UR) = 5.7%
Std(UR) = 1.7%
Skew(UR) = 0.9
Kurt(UR) = 1.1
min(UR) = 2.5%
max(UR) = 14.8%

# Plot histogram
fig, ax = plt.subplots(figsize=(6.5,2.5));
ax.hist(data.UR,edgecolor='black',density='true')
ax.set_xlabel('U.S. Unemployment Rate');
ax.set_ylabel('probability')
ax.xaxis.set_major_formatter('{x:,.1f}%')
ax.grid(); ax.autoscale(tight=True)
_images/f0c9aa8f71d9367b217080f62d5f521f8a02f412b29f850a7c55ee7fd1503b19.png

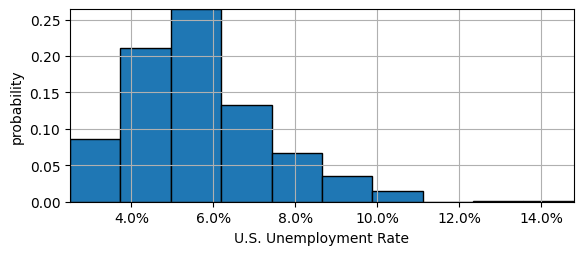
  • Most recent UR is \(4.1\%\), or \(1.6pp\) below historical mean of \(5.7\%\)

  • Std. Dev. is \(1.7\%\). If UR was normally distributed, then \(\pm 2 SD\), or interval from \(0.7\%\) to \(9.1\%\), would contain \(95\%\).

  • But minimum UR is \(2.5\%\) and maximum is \(14.8\%\), which indicates UR is most likely skewed.

  • \(Skew(UR) = 0.9\) and we see that histogram has long right tail.

Key Concepts#

  • White Noise is a special type of time series, where the values are random and uncorrelated across time.

  • Stationarity, e.g., does the data have a trend, seasonality, or is the covariance changing over time? If no to all, then it is stationary.

  • If the data is non-stationary, then the underlying probabilistic structure of the series is changing over time, and there is no way to relate the future to the past.

  • A Random Walk is a key model for the log price of a financial asset.

  • Autocorrelation is a measure of how values in a time series are correlated with previous values.

Contents