Review 1B Key

Contents

Review 1B Key#

by Professor Throckmorton
for Time Series Econometrics
W&M ECON 408/PUBP 616
Slides

1)#

  • Read U.S. Industrial Production: Total Index (IPB50001N) from FRED.

  • Resample/reindex the data to a quarterly frequency using the value for the last month of each quarter.

  • Print the original data and compare it to the resampled/reindexed data to verify it is correct.

# Libraries
from fredapi import Fred
import pandas as pd
# Read data
fred_api_key = pd.read_csv('fred_api_key.txt', header=None)
fred = Fred(api_key=fred_api_key.iloc[0,0])
data = fred.get_series('IPB50001N').to_frame(name='IP')
print(data.tail(3))
# Resample/reindex to quarterly frequency
data = data.resample('QE').last()
# Print data
print(f'number of rows/quarters = {len(data)}')
print(data.tail(3))

                  IP
2025-06-01  105.4026
2025-07-01  104.3398
2025-08-01  106.0004
number of rows/quarters = 427
                  IP
2025-03-31  104.1248
2025-06-30  105.4026
2025-09-30  106.0004

2)#

  • Why is this data not stationary?

  • Use appropriate transformations to remove the non-stationarity and plot the series.

  • Correctly and completely label the plot.

# Plotting
import matplotlib.pyplot as plt
# Plot
fig, ax = plt.subplots(figsize=(6.5,2));
ax.plot(data.IP);
ax.set_title('Industrial Production (Index, Quarterly)');
ax.grid(); ax.autoscale(tight=True)
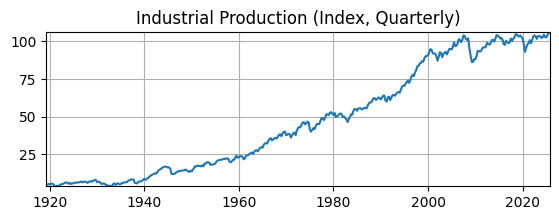
_images/d9aee880dd8ca511798e89839944b5b8b11c36a0e0b19f53d208dd8c9a2de18d.png

This data is non-stationary because it is seasonal over the year and it has an exponential time trend.

# Scientific computing
import numpy as np
# Transform data
#    Take log
data['logIP'] = np.log(data.IP)
#    Take difference
data['dlogIP'] = 100*(data.logIP.diff(4))

# Plot
fig, ax = plt.subplots(figsize=(6.5,2.5));
ax.plot(data.dlogIP);
ax.set_title('Industrial Production (YoY % Change, Quarterly)');
ax.yaxis.set_major_formatter('{x:.0f}%')
ax.grid(); ax.autoscale(tight=True)
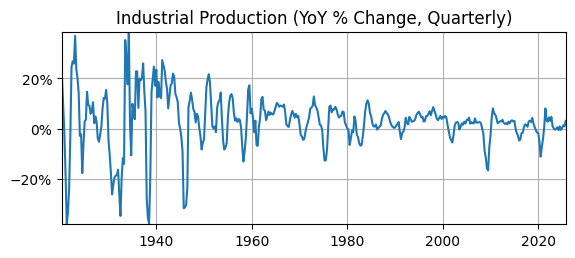
_images/9461a039a05d2af5cc17e110e20323a87557702b1ce3be759e815e5360d0f760.png

Time varying volatility indicates this is non-stationary data.

3)#

  • Plot the autocorrelation function of the transformed data.

  • Is it stationary? Why or why not?

#   Auto-correlation function
from statsmodels.graphics.tsaplots import plot_acf as acf
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,2))
acf(data.dlogIP.dropna(),ax)
ax.grid(); ax.autoscale(tight=True)
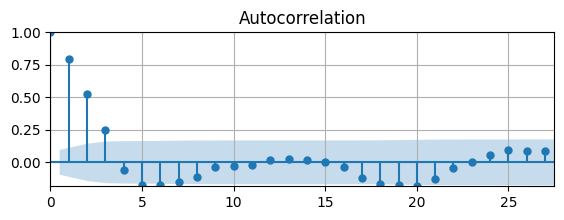
_images/1d15c89b6d691a34745990936487142ddf15e9b0d6704ee62aca1254caabe65e.png

  • ACF is signifcant at long lags, doesn’t clearly taper to zero

  • might be non-stationary

  • First 3 lags are remarkable

4)#

  • Conduct a unit root test of the transformed data.

  • Is it stationary? Why or why not?

# ADF Test
from statsmodels.tsa.stattools import adfuller
# Function to organize ADF test results
def adf_test(data):
    keys = ['Test Statistic','p-value','# of Lags','# of Obs']
    values = adfuller(data)
    test = pd.DataFrame.from_dict(dict(zip(keys,values[0:4])),
                                  orient='index',columns=[data.name])
    return test
adf_test(data.dlogIP.dropna())
dlogIP
Test Statistic -5.814992e+00
p-value 4.313232e-07
# of Lags 1.500000e+01
# of Obs 4.070000e+02

  • Null hypothesis: data has unit root

  • p-value near zero, so reject the null

  • Unit root test says data is probably stationary

5)#

If you were to pick a parsimonious AR model (i.e., the number of lags is less than 5) to fit the transformed data, what lag would you pick? Why?

# Partial auto-correlation function
from statsmodels.graphics.tsaplots import plot_pacf as pacf
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
pacf(data.dlogIP.dropna(),ax)
ax.grid(); ax.autoscale(tight=True);
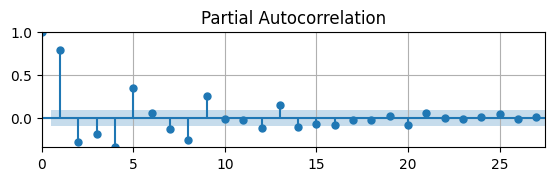
_images/ac3ac63922a58f5dc444b0dbed7ead2eaa2547ecba97f05cc3ea6778ff999f5e.png

  • PACF is signficantly different from zero for first 5 lags

  • Stops being signficant for lag 6

6)#

  • Given your last answer, estimate an AR model given the transformed quarterly data.

  • Interpret the results.

# ARIMA model
from statsmodels.tsa.arima.model import ARIMA
# Define model
mod = ARIMA(data.dlogIP,order=(5,0,0))
# Estimate model
res = mod.fit()
summary = res.summary()
# Print summary tables
tab0 = summary.tables[0].as_html()
tab1 = summary.tables[1].as_html()
tab2 = summary.tables[2].as_html()
#print(tab0); print(tab1); print(tab2)
Dep. Variable: dlogIP No. Observations: 425
Model: ARIMA(5, 0, 0) Log Likelihood -1298.814
coef std err z P>|z| [0.025 0.975]
const 2.9265 0.975 3.002 0.003 1.016 4.837
ar.L1 1.0243 0.031 32.647 0.000 0.963 1.086
ar.L2 -0.1735 0.042 -4.163 0.000 -0.255 -0.092
ar.L3 0.1902 0.035 5.505 0.000 0.123 0.258
ar.L4 -0.6642 0.029 -22.871 0.000 -0.721 -0.607
ar.L5 0.3486 0.025 13.773 0.000 0.299 0.398
sigma2 27.8385 0.912 30.511 0.000 26.050 29.627
Heteroskedasticity (H): 0.05 Skew: 0.34
Prob(H) (two-sided): 0.00 Kurtosis: 13.72

  • All the AR coefficients are significantly different than zero

  • Residuals have a lot of kurtosis, so maybe AR model isn’t the best choice

Contents