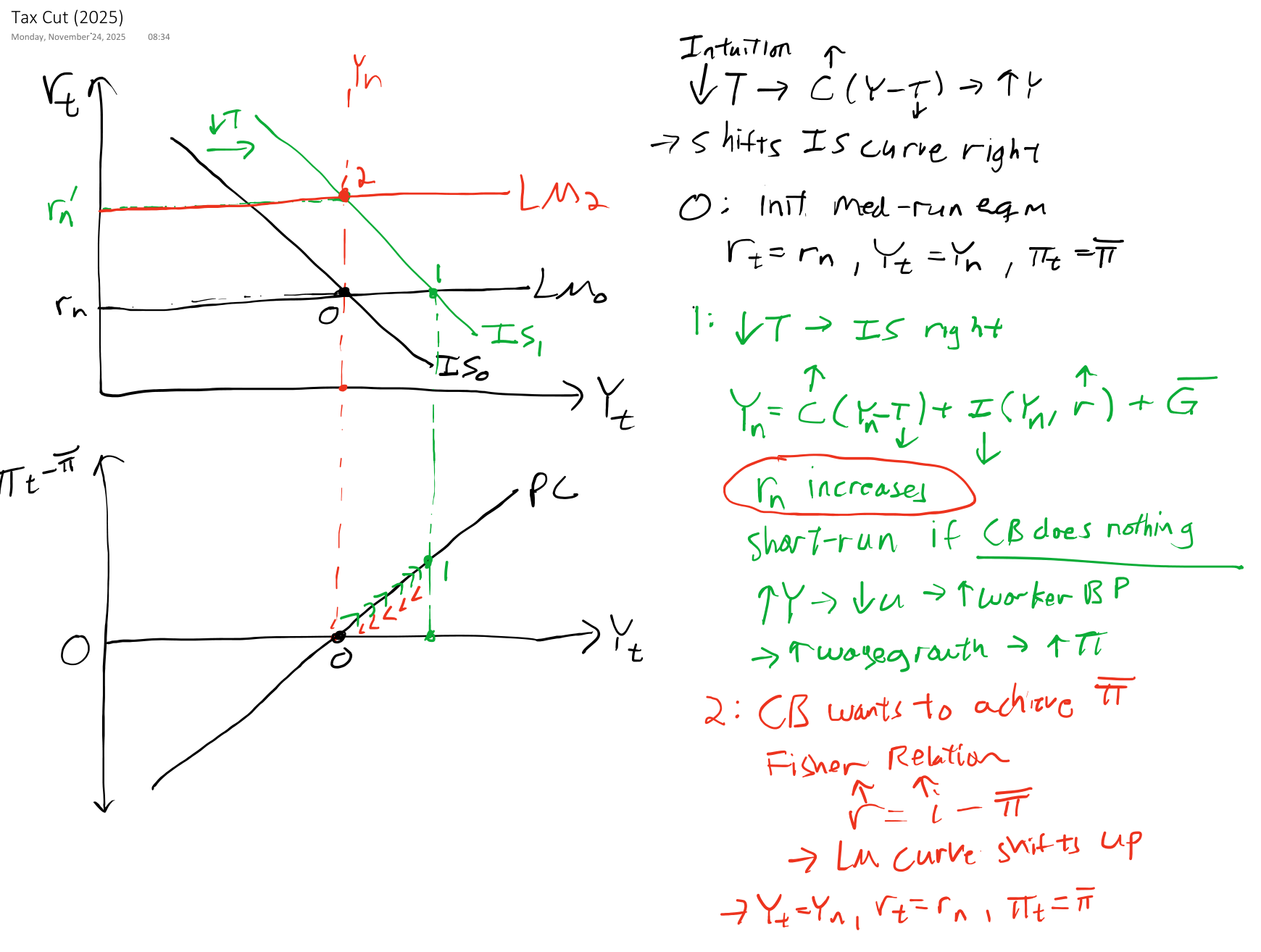
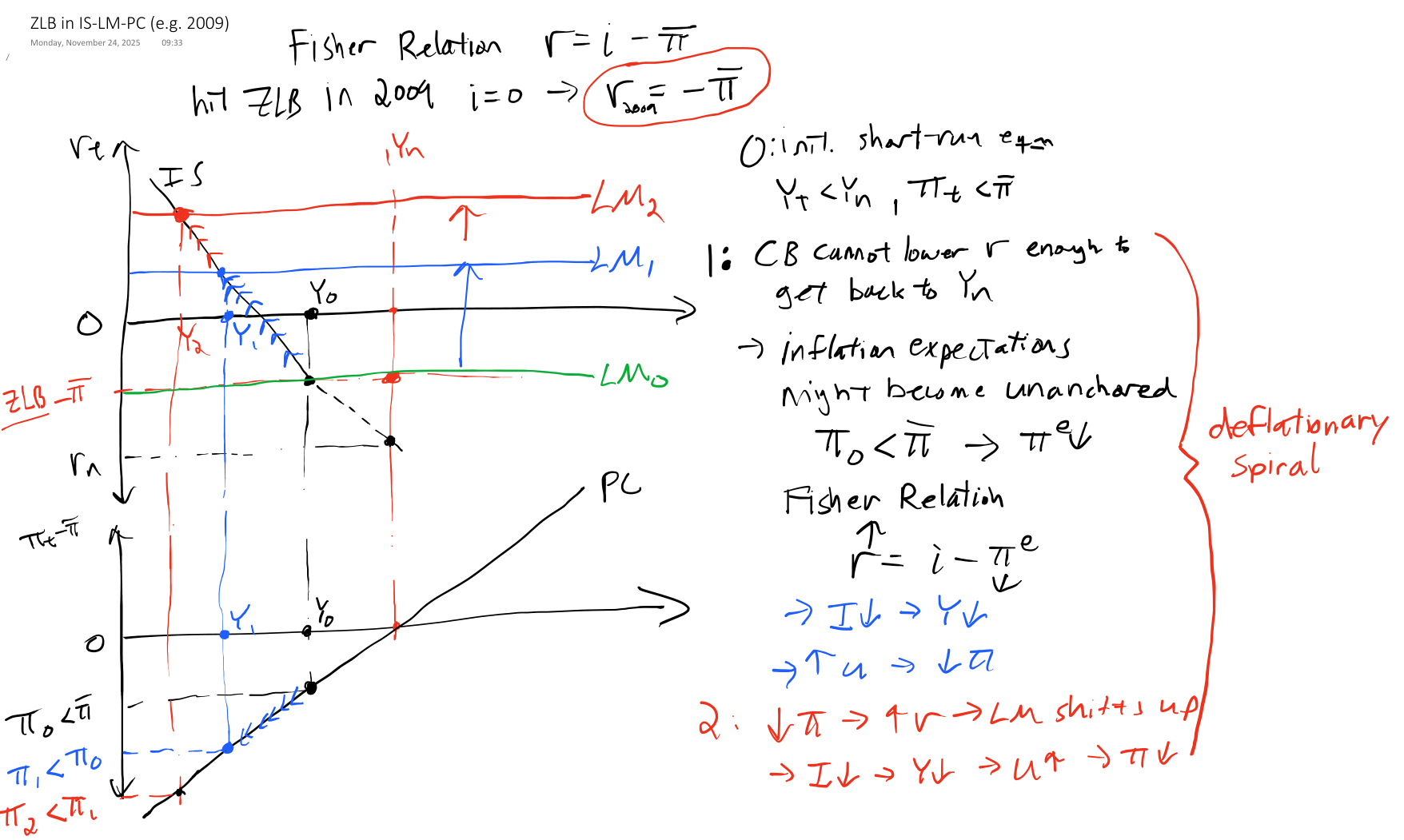
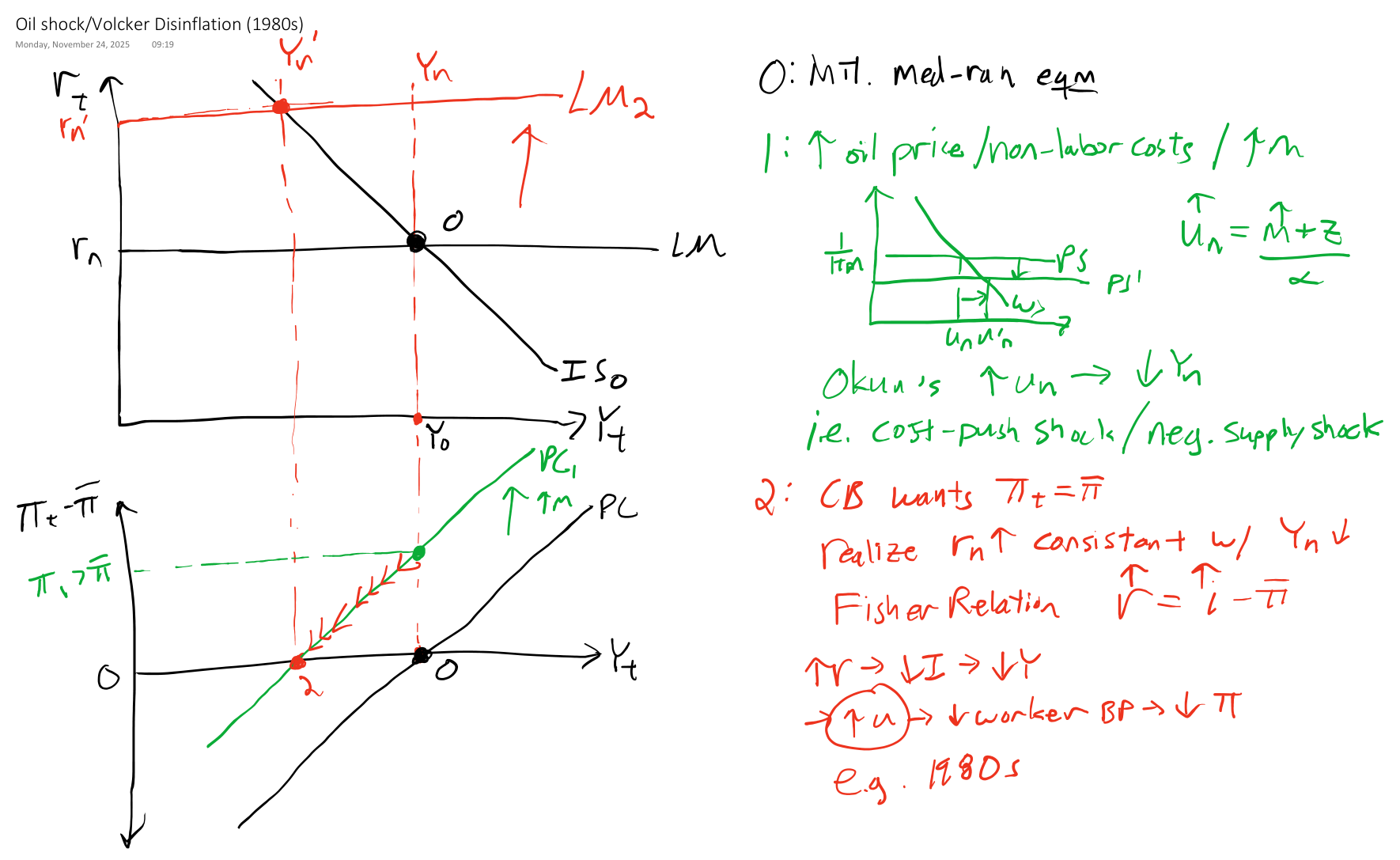
IS-LM-PC Model - Intermediate Macro

by Professor Throckmorton
for Intermediate Macro
W&M ECON 304
Slides

Summary¶

Okun’s Law: negative relationship between output, $Y$ , and the unemployment rate, $u$
Real vs. nominal interest rate and the medium-run IS-LM-PC equilibrium
IS-LM-PC: short-run vs. medium-run equilibrium
Q: What does a recession look like in the model?
The ZLB and Deflationary Spirals

Okun’s Law¶

IS-LM model is in the $(\pi,Y)$ space, but Phillips Curve is in the $(\pi,u)$ space.
To combine IS-LM and PC, we will first transform the PC into the $(\pi,Y)$ space.
To do that, we need Okun’s law, which is a negative relationship between output, $Y$ , and unemployment rate, $u$ , relative to the medium-run equilibrium

Recall these labor market definitions: $L = U + N$ and $u = U/L$
For the labor market, we assumed the production function is $Y = N$ , so we can also substitute $N$ out for $Y$ ,
$\begin{gather*} u = \frac{U}{L} = \frac{L - N}{L} = 1 - \frac{Y}{L} \end{gather*}$
(1)
i.e., unemployment rate and output are negatively related (by definition)
Rearrange and add time subscripts (assuming $L$ is constant in short run)
$\begin{gather*} u = 1 - Y/L \quad \rightarrow \quad Y_t = L(1 - u_t) \end{gather*}$
(2)
Note that equation also holds in the medium run, $Y_n = L(1 - u_n)$ , i.e., the natural unemployment rate implies a natural, or potential, output level.

Subtract the medium-run equation from the short-run equation:
$\begin{align*} \rightarrow Y_t - Y_n &= -L(u_t - u_n) \\ \textrm{or} \quad u_t - u_n &= - \frac{1}{L}(Y_t - Y_n) \end{align*}$
(3)
This is Okun’s Law.
Substitute Okun’s Law into Phillips Curve
$\begin{align*} \pi_t - \pi_t^e &= - \alpha (u_t - u_n) \\ \rightarrow \pi_t - \pi_t^e &= \frac{\alpha}{L} (Y_t - Y_n) \end{align*}$
(4)

Inflation vs. Output¶

Again, suppose $\pi_t^e = \bar{\pi}$ , i.e., expectations are anchored, and the central bank is credible
$\begin{gather*} \pi_t - \bar{\pi} &= \frac{\alpha}{L} (Y_t - Y_n) \end{gather*}$
(5)
- If $Y_t = Y_n$ (eqm), then $\pi_t$ is stable at the Fed’s target
- If $Y_t < Y_n$ (recession), then $\pi_t$ falls below the Fed’s target
- If $Y_t > Y_n$ (boom), then $\pi_t$ rises above the Fed’s target
This version of the Phillips Curve appears in the IS-LM-PC model and is equation 9.4 in Blanchard, Macroeconomics (9th Edition, 2025).

Real vs. Nominal Interest Rate¶

Recall the simple loan example from the Money Market. Suppose you lend me $P_t$ dollars, and next year I will pay you back
$\begin{gather*} \textrm{principal} + \textrm{interest} = P_t + i_tP_t = (1+i_t)P_t \end{gather*}$
(6)
where the nominal interest rate, $i_t$ , we agree on ahead of time
Q: What is the real value of that future payment today?
A:
$\begin{gather*} \frac{\textrm{\$ received in future}}{\textrm{expected \$ price of goods}} = \frac{(1+i_t)P_t}{P_{t+1}^e} \equiv 1 + r_t \end{gather*}$
(7)
- $P_{t+1}^e$ : expected price of goods and services next year
- $r_t$ : the real interest rate (in terms of goods, not dollars)
Problems: It’s not in terms of the inflation rate. And it’s a nonlinear relationship, which is difficult to use/interpret.

Substitute in inflation rate

Recall the definition of the inflation rate

\begin{align*} \pi_t &= P_t/P_{t-1} - 1 \\ \rightarrow \pi_{t+1} &= P_{t+1}/P_t - 1 \\ \rightarrow \pi_{t+1}^e &= P_{t+1}^e/P_t - 1 \\ \rightarrow 1+ \pi_{t+1}^e &= P_{t+1}^e/P_t \\ \rightarrow \frac{P_t}{P_{t+1}^e} &= \frac{1}{1+ \pi_{t+1}^e} \end{align*}

(8)

Combine that with real interest rate

\begin{gather*} 1 + r_t = \frac{1+i_t}{1+\pi_{t+1}^e} \end{gather*}

(9)

Nonlinear $\rightarrow$ linear

Recall the properties of natural log
$\begin{align*} \log(X/Y) &= \log(X) - \log(Y) \\ \log(1+X) &\approx X \textrm{ if $X$ is small} \end{align*}$
(10)
Take natural log of both sides
$\begin{gather*} \log(1 + r_t) = \log (1+i_t) - \log (1+\pi_{t+1}^e) \end{gather*}$
(11)
Note $0 < r_t,i_t,\pi_{t+1}^e < 0.10$ are small
Approximate $\log(1+X) \approx X$ (since $X$ is small)
$\begin{gather*} r_t \approx i_t - \pi_{t+1}^e \end{gather*}$
(12)
i.e., the real interest rate equals the nominal rate minus expected inflation

Fisher Relation Examples

Fisher Relation
$\begin{gather*} r_t = i_t - \pi_{t+1}^e \end{gather*}$
(13)
Note that $i_t \geq 0$ in the U.S.
2008-2015: Suppose $i_t = 0\%$ and $\pi_{t+1}^e = 1.75\%$ (annual rates)
$\begin{gather*} r_t = 0\% - 1.75\% = - 1.75\% \end{gather*}$
(14)
Note the real interest rate can be negative!
Great Depression: $i_t = 0\%$ and $\pi_{t+1}^e < 0\%$ (deflation)
$\begin{gather*} r_t = 0\% - \textrm{ something negative} = \textrm{ something positive} \end{gather*}$
(15)
Note that the real interest rate can be greater than the nominal rate, and that really hurts borrowers! (debt deflation)

Data Example

# This script began as a copy-paste from a previous script in this book
# Then it was modified with the help of GitHub Copilot
# Finally, it was manually edited for accuracy and aesthetics

# Libraries
from fredapi import Fred
import pandas as pd
# Read data
fred_api_key = pd.read_csv('fred_api_key.txt', header=None).iloc[0,0]
fred = Fred(api_key=fred_api_key)
data = fred.get_series('DGS10').to_frame(name='10Y Treasury Yield')
# append unemployment rate to data
data['10Y TIPS Yield'] = fred.get_series('DFII10')
# append difference column to data
data['Expected Inflation Rate'] = data['10Y Treasury Yield'] - data['10Y TIPS Yield']
# reindex data to QE by averaging quarterly
data = data.resample('QE').mean()
# remove data before 2003
data = data[data.index.year >= 2003]

# create list with 3 line types, one for each column
line_types = ['--b', '--r', '-k']
# plot all columns of data with loop
import matplotlib.pyplot as plt
plt.figure(figsize=(8.5,4))
for i, column in enumerate(data.columns):
    plt.plot(data.index, data[column], line_types[i], label=column)
plt.xlabel('Year')
plt.ylabel('Annual Rate')
plt.legend()
# add grid lines
plt.grid()
# orient legend horizontally and relocate to outside top center
plt.legend(loc='upper center', ncol=len(data.columns), bbox_to_anchor=(0.5, 1.15))
# set xlims to 2003-04-01 to 2025-9-30
plt.xlim(pd.Timestamp('2003-04-01'), pd.Timestamp('2025-09-30'))
# add % to ylabels
plt.gca().yaxis.set_major_formatter(plt.FuncFormatter(lambda y, _: '{:.0f}%'.format(y)))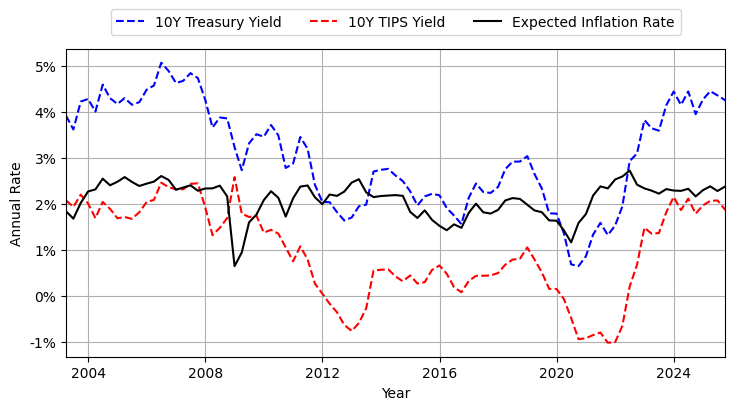

10Y TIPS principal is indexed to inflation, so price is higher than 10Y (non-indexed) Treasury and yield is lower.
Difference in yields is a measure of expected inflation rate (which is an application of the Fisher relation)
Implied expected inflation rate is usually the Fed’s target of 2%

Goods Market in medium-run¶

Medium-run equilibrium defined by (Labor Market, PC, and Okun’s Law)

\begin{gather*} \pi_t^e = \bar{\pi} \rightarrow u_t = u_n \rightarrow Y_t = Y_n \end{gather*}

(16)

Substitute into goods market short-run equilibrium
$\begin{gather*} Y_n = C(c_0,Y_n,T) + I(b_0,Y_n,r_t) + G \end{gather*}$
(17)
Note investment is function of real interest rate.
Assuming $c_0$ , $b_0$ , $G$ , and $T$ are fixed, then the only other variable in equation is $r$ . Thus,
$\begin{gather*} r_t = r_n \end{gather*}$
(18)
in a medium-run equilibrium.
$r_n$ is the natural real interest rate, often called the “neutral rate” since $\pi_t = \bar{\pi}$ when $r_t = r_n$ .

IS-LM-PC Graph¶

# This script began as a ChatGPT-5.1 translation of a hand-drawn figure
# It was then modified with the help of GitHub Copilot
# It was then manually edited for accuracy and aesthetics
import numpy as np
import matplotlib.pyplot as plt

# Set up figure
fig, axes = plt.subplots(2, 1, figsize=(6, 6))

# -------------------------
# 1. IS–LM diagram (top)
# -------------------------
ax1 = axes[0]

# Axes limits
xmax = 10
ymax = 6
ax1.set_xlim(0, xmax)
ax1.set_ylim(0, ymax)

# Remove ticks
ax1.set_xticks([])
ax1.set_yticks([])

# Draw axes manually
#ax1.axhline(0, color='black', linewidth=2)
ax1.axvline(0, color='black', linewidth=2)

# Equilibrium point
Yn = 5
rn = 3

# Vertical red line at Yn
ax1.axvline(Yn, color='red', linestyle='--', linewidth=1.5)

# IS curve
Y = np.linspace(1, xmax-1, 100)
IS = rn - 0.7*(Y - Yn)
ax1.plot(Y, IS, color='black')

# LM curve
LM = rn + 0*(Y - Yn)
ax1.plot(Y, LM, color='black')

# Equilibrium point
ax1.plot(Yn, rn, 'ko')

# Labels
ax1.text(xmax+.2, -0.5, "$Y_t$", fontsize=12)
ax1.text(-0.7, 6, "$r_t$", fontsize=12)
ax1.text(8, rn+.2, "LM", fontsize=12)
ax1.text(8, rn-2, "IS", fontsize=12)
ax1.text(Yn + 0.1, 5.5, "$Y_n$", color="red", fontsize=12)
ax1.text(Yn, -0.5, "$Y_0$", fontsize=12, ha='center')
ax1.text(-0.3, rn, "$r_0 = r_n$", fontsize=12, va='center',ha='right')

# -------------------------
# 2. Phillips Curve diagram (bottom)
# -------------------------
ax2 = axes[1]

# Axes limits
ax2.set_xlim(0, 10)
ax2.set_ylim(-5, 5)

# Remove ticks
ax2.set_xticks([])
ax2.set_yticks([])

# Draw axes manually
ax2.axhline(0, color='black', linewidth=2)
ax2.axvline(0, color='black', linewidth=2)

# Vertical red line at Yn
ax2.axvline(Yn, color='red', linestyle='--', linewidth=1.5)

# Phillips curve
PC = 0 + 1*(Y - Yn)
ax2.plot(Y, PC, color='black')

# Equilibrium point
ax2.plot(Yn, 0, 'ko')

# Labels
ax2.text(xmax+.2, -1, "$Y_t$", fontsize=12, va='center')
ax2.text(-.3, 5, r"$\pi_t-\bar{\pi}$", fontsize=12,ha='right')
ax2.text(8, 3.8, "PC", fontsize=12)
ax2.text(Yn, -1, "$Y_0$", fontsize=12, ha='center')
ax2.text(-.3, 0, "0", fontsize=12, va='center',ha='right')

# remove upper and right box from both plots
for ax in axes:
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

# remove bottom box from bottom plot
axes[1].spines['bottom'].set_visible(False)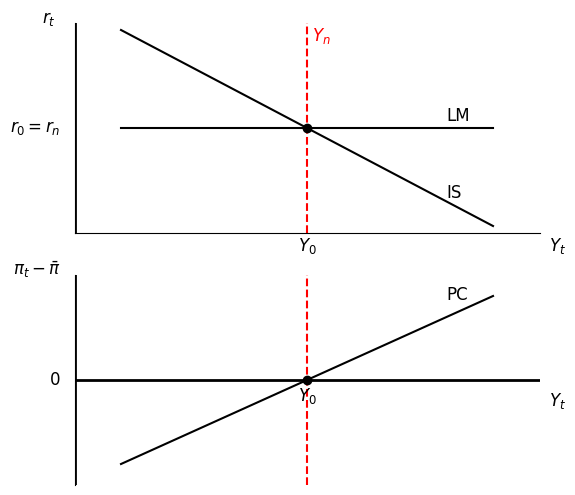

Experiments¶