Phillips Curve

by Professor Throckmorton
for Intermediate Macro
W&M ECON 304
Slides

Summary¶

1. Phillips Curve: negative relationship b/t inflation ($\pi_t$) and unemployment ($u_t$),
   i.e., if central bank wants lower inflation, then the economy must make the sacrifice of higher unemployment

2. Testing the Phillips Curve in the United States

   • 1960s: low and stable inflation, i.e., $\pi^e \approx 0 \rightarrow corr(\pi_t,u_t) < 0$

   • 1970 to 1995: big positive oil price shocks, $\uparrow \pi \rightarrow \uparrow \pi^e \rightarrow \uparrow \pi$

   • 1996 to 2019: Fed achieves goal of $\pi^e \approx 2$

3. Phillips Curve can be expressed relative to the medium-run equilibrium

Starting from Labor Market¶

• The Phillips Curve comes from the Labor Market

  $$\begin{gather*} W = P^e F(u,z) \\ P = (1+m)W \end{gather*}$$

  (1)

  and the medium-run equilibrium determines the natural rate of unemployment.

• Right now $P$ shows up, but we want relationship between $\pi$ and $u$. Recall for Chapter 2

  $$\begin{gather*} \pi_t = P_t/P_{t-1} -1 \end{gather*}$$

  (2)

Adding time and the inflation rate

1. Want: relationship b/t $\pi$ and $u$

2. Substitute WS into PS

   $$\begin{gather*} P = (1+m)P^e F(u,z) \end{gather*}$$

   (3)

3. Add time subscripts and divide by $P_{t-1}$

   $$\begin{gather*} P_t/P_{t-1} = (1+m)(P_t^e/P_{t-1}) F(u_t,z) \end{gather*}$$

   (4)

   where $m$ and $z$ are constant w.r.t. time

4. Note from definition of $\pi_t$ that

   $$\begin{gather*} P_t/P_{t-1} = 1 + \pi_t \end{gather*}$$

   (5)

   and similarly

   $$\begin{gather*} P_t^e/P_{t-1} = 1 + \pi_t^e \end{gather*}$$

   (6)

Combine equations

5. Combine results from steps 3. and 4.

   $$\begin{gather*} 1 + \pi_t = (1+m)(1 + \pi_t^e) F(u_t,z) \end{gather*}$$

   (7)

   That’s difficult to interpret. It is a nonlinear equation, e.g., $\pi_t^e$ multiplies $u_t$.

6. What is worker bargaining power, $F(u_t,z)$? Remember $\uparrow u_t \rightarrow \downarrow worker B.P.$. Let’s assume

   $$\begin{gather*} F(u_t,z) = 1 - \alpha u_t + z \end{gather*}$$

   (8)

7. Substitute out worker bargaining power function

   $$\begin{gather*} 1 + \pi_t = (1+m)(1 + \pi_t^e) (1 - \alpha u_t + z) \end{gather*}$$

   (9)

   This is still nonlinear.

Approximate linearly

• We’ll use natural logs to approximate the Phillips curve linearly. In disciplines that use dynamic models, e.g., economics, physics, and biology, this is known as log-linearizing.

• Recall some facts about logs from math class:

  $$\begin{gather*} \log(XY) = \log(X) + \log(Y) \\ \log(1+X) \approx X \textrm{ if $X$ is small} \end{gather*}$$

  (10)

Apply properties of logs

8. Apply $\log(XY) = \log(X) + \log(Y)$

   $$\begin{align*} 1 + \pi_t &= (1+m)(1 + \pi_t^e) (1 - \alpha u_t + z) \\ \rightarrow \log(1 + \pi_t) &= \log(1+m) + \log(1 + \pi_t^e) + \log(1 - \alpha u_t + z) \end{align*}$$

   (11)

9. Note $0.10 < m < 0.20$. Also $0 < \pi < 0.10$, and the same is true for $\pi^e$, $u$, and $z$, i.e., they are relatively small.

10. Apply $\log(1+X) \approx X$.

    $$\begin{gather*} \pi_t \approx \pi_t^e - \alpha u_t + m + z \end{gather*}$$

    (12)

    This is equation 8.2 in Blanchard, Macroeconomics (9th Edition, 2025).

Phillips Curve (PC)¶

• Properties of the Phillips Curve all relate to Labor Market

  • $\uparrow \pi_t^e \rightarrow \uparrow \pi_t$: If workers expect prices to rise, then they will demand higher wages, which leads firms to eventually raise prices. Thus the expectation is self-filling.

  • $\uparrow m \rightarrow \uparrow \pi_t$: If firms markup of price above cost rises, then prices are growing faster.

  • $\uparrow z \rightarrow \uparrow \pi_t$: Any policies that increase worker bargaining power will allow workers to demand high wages, driving up costs and prices.

An Experiment

• We defined $m$ as the markup, but we can also interpret it as any non-labor costs.

• In the 1970s United States, we saw a 5-fold increase in the price of oil.

• That kind of shock is known as a “cost-push” shock, which is inflationary, and shifts up the PC.

• If inflation remains high for too long, then people begin to expect higher inflation, which shifts up the PC again due to a wage-price spiral.

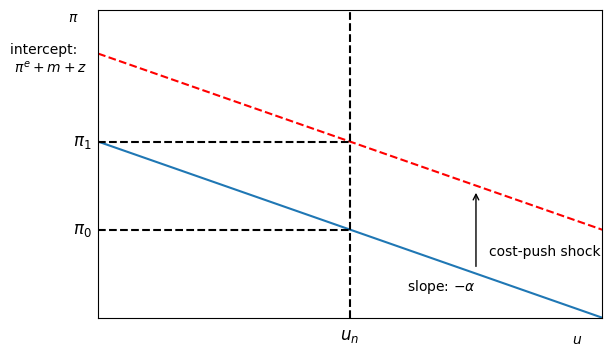
• An increase in $m$ shifts up the PC

• At $u_n$, inflation rises from $\pi_0$ to $\pi_1$

• We know from labor market that $\uparrow m \rightarrow \uparrow u_n$.

• Thus $\alpha$ tells us how much $u$ must rise for inflation to return to $\pi_0$.

• The PC would also shift up if $\pi^e \uparrow$

Testing the PC¶

The Phillips Curve is a testable hypothesis (i.e., linear regression)

The test is whether $\alpha$ is statistically significantly positive when controlling for expected inflation.

• $\pi_t$: current inflation

• $\pi_t^e$: expected inflation (measured by market/survey data)

• $\alpha$: sensitivity of wages demanded to the business cycle

• $u_t$: current unemployment (summarizes the business cycle)

• $m$: markup of price over cost

• $z$: other things that affect worker bargaining power

Expected Inflation

• In practice, there are two popular measures of expected inflation

  1. Survey data: ask people for their inflation forecasts, e.g., Philadelphia Fed Survey of Professional Forecasters

  2. Market data: observe difference in bond prices on nominal bonds and inflation-indexed bonds. Inflation-index bonds are officially called Treasury Inflation Protected Securities (TIPS).

• In theory, we can simplify the model with an assumption about expected inflation

  1. Assume expected inflation is anchored to some value, $\pi_t^e = \bar{\pi}$.

  2. Assume expected inflation is adapting to recent data, $\pi_t^e = \pi_{t-1}$.

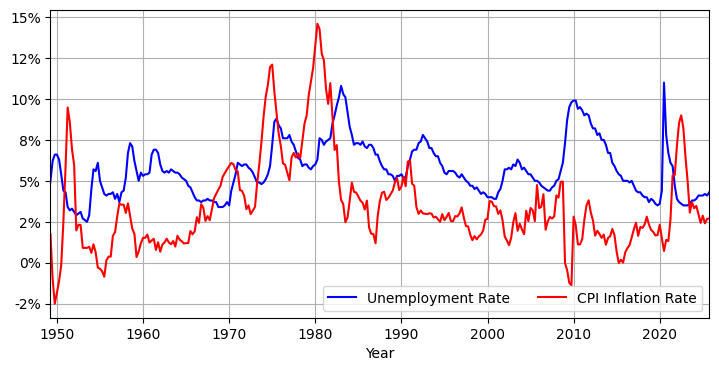
• Inflation is low and stable around 1% in early-mid 1960s.

• It is safe to assume that at that time expected inflation was anchored to 1%.

The 1960s¶

• Notice inflation in early 1960s is about $1\%$ (low and stable)

• Let’s assume people are forming expectations given what they observe:

  $$\begin{gather*} \pi_t^e = \bar{\pi} \approx 1\% \end{gather*}$$

  (15)

  i.e., expectations are anchored at some value

• Phillips curve becomes

  $$\begin{gather*} \pi_t = \bar{\pi} -\alpha u_t + m + z \end{gather*}$$

  (16)

• If the assumption that worker bargaining power is countercyclical, i.e., $\uparrow u_t \rightarrow \downarrow \textrm{ worker } B.P.$, is good, then Phillips curve predicts:

  $$\begin{gather*} \textrm{Corr}(\pi_t,u_t) < 0 \end{gather*}$$

  (17)

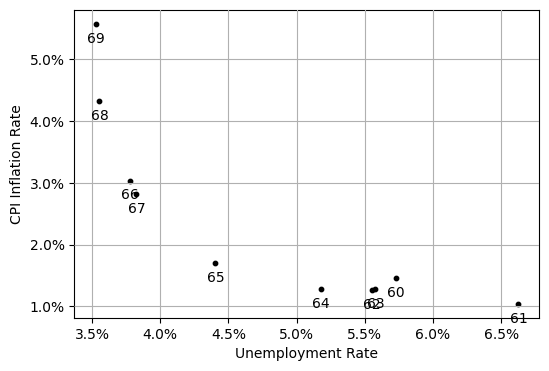
• In 1960s, obvious negative relationship between inflation and unemployment.

• Relationship looks nonlinear since the unemployment rate cannot fall further.

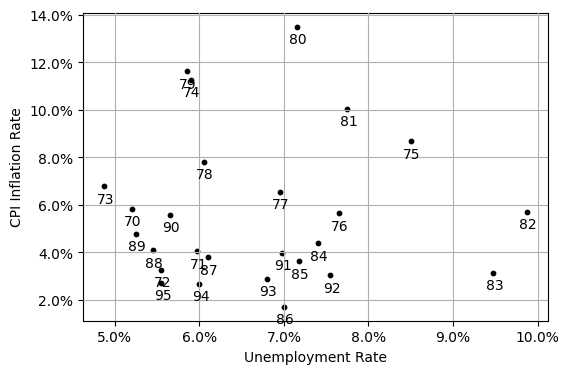
• After 1960s, no clear relationship between inflation and unemployment.

• Q: Is the Phillips curve irrelevant?

• A: It depends on how people form expectations.

1970 to 1995¶

• Big positive oil price shocks cause inflation to rise rapidly

• People form expectations given what they observe:

  $$\begin{gather*} \pi_t^e = \pi_{t-1} \end{gather*}$$

  (18)

  i.e., expectations have become unanchored from a particular value

• Phillips curve becomes

  $$\begin{align*} \pi_t &= \pi_{t-1} -\alpha u_t + m + z \\ \pi_t - \pi_{t-1} &= -\alpha u_t + m + z \\ \Delta \pi_t &= -\alpha u_t + m + z \end{align*}$$

  (19)

  where $\Delta \pi_t \equiv \pi_t - \pi_{t-1}$.

• The Phillips curve predicts:

  $$\begin{gather*} \textrm{Corr}(\Delta \pi_t ,u_t) < 0 \end{gather*}$$

  (20)

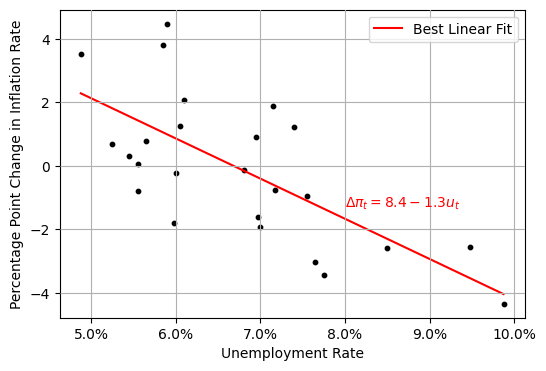
• Each point is a year between 1970 and 1995.

• The vertical axis is the first difference of the inflation rate.

• The $p$-value on the slope is close to zero, so the slope is statistically significantly different from zero.

1996 to 2019¶

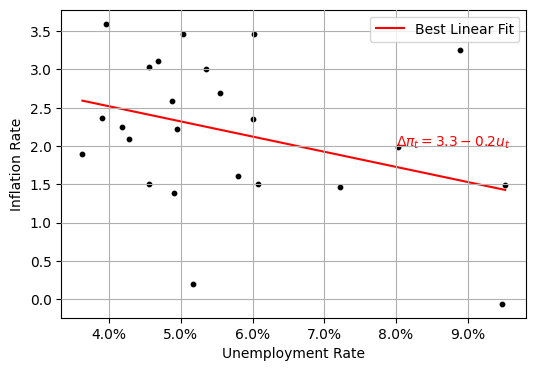
• In early 1990s, Fed settles on $2\%$ inflation target

• Fed (mostly) successfully achieves and maintains target from 1996 to 2019

• Inflation expectations are anchored, $\pi^e \approx 2\%$

• Thus, the best model for the PC is the same as 1960s

Medium-run Equilibrium¶

• Substitute $\pi_t = \pi_t^e$ and $u_t = u_n$ into Phillips curve

  $$\begin{gather*} \pi_t = \pi_t - \alpha u_n + m + z \end{gather*}$$

  (21)

• Solve for $u_n$

  $$\begin{gather*} u_n = (m + z)/\alpha \end{gather*}$$

  (22)

• The equilibrium/natural unemployment rate increases if

  • the markup increases

  • worker B.P. increases (not because of the business cycle)

  • the sensitivity of wages demanded to an increase in B.P. falls

1. Want: Phillips Curve relative to eqm so we can study how inflation responds to events/policy changes

2. Substitute $u_n = (m + z)/\alpha$ into Phillips curve

   $$\begin{align*} \pi_t &= \pi_t^e - \alpha u_t + {\color{red}\alpha}\frac{m + z}{\color{red}\alpha} \\ \pi_t &= \pi_t^e - \alpha u_t + \alpha u_n \end{align*}$$

   (23)

3. Rearranging/simplifying

   $$\begin{gather*} \pi_t - \pi_t^e &= - \alpha (u_t - u_n) \end{gather*}$$

   (24)

• Suppose $\pi_t^e = \bar{\pi}$ (as supported by data from 1996 to 2019, and hopefully from 2024 onward)

  $$\begin{align*} \pi_t - \bar{\pi} &= - \alpha (u_t - u_n) \end{align*}$$

  (25)

• Interpretation

  • If $u_t = u_n$ (eqm), then $\pi_t$ is stable at the target

  • If $u_t > u_n$ (not eqm), then $\pi_t$ is below the target

  • If $u_t < u_n$ (not eqm), then $\pi_t$ is above the target

• The last two, if sustained for a significant time, may erode the central bank’s credibility and possibly unanchor expectations.