AR Model
by Professor Throckmorton
for Time Series Econometrics
W&M ECON 408
Slides
AR() Model¶
The AR() model is:
, , , are the autoregressive parameters that quantify the influence of past values on the current value
is white noise error term (or innovation) with mean zero and constant variance,
AR(1) Model¶
An AR(1) Model is a special case of the AR()
An AR(1) is often used to model cyclical dynamics
e.g., the fluctuations in an AR(1) series where appear much more persistent (i.e., smoother) than those where
AR(1) for any mean¶
An AR(1) model is covariance stationary if
Suppose
Then since
Instead consider the AR(1) model with a generic mean:
Then since
You can rearrange the (any mean) AR(1) model as
AR(1) as MA()¶
The AR(1) model structure is the same at all points in time
Combine, i.e., recursively substitute, to get
Rinse and repeat to get (i.e., the MA() Model or Wold Representation)
And an MA() is invertible back to an AR(1) so long as .
An AR model that can be written as an MA() is causal (or exhibits causality).
That property differentiates it from an invertible MA model, which can be expressed as an AR() model.
Variance¶
Suppose without loss of generality.
Given and , then
See Geometric Series.
Autocorrelation¶
In general, , which is a very nice looking ACF.
Thus, for an AR(1) process/model we can refer to as the autocorrelation (AC) parameter/coefficient.
AR Model as DGP¶
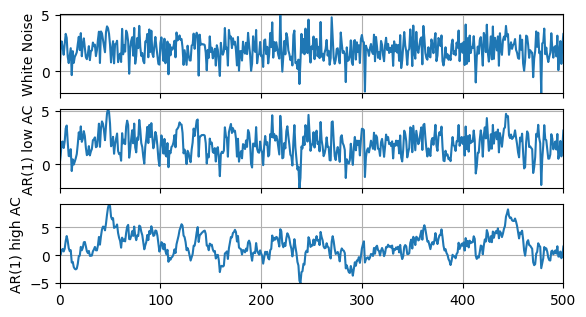
Let’s compare a couple different AR models to their underlying white noise.
White noise:
AR(1), low AC:
AR(1), high AC:
# Libraries
import numpy as np
# Assign parameters
T = 501; mu = 2; phi_l = 0.5; phi_h = 0.9;
# Draw random numbers
rng = np.random.default_rng(seed=0)
eps = rng.standard_normal(T)
# Simulate time series
y = np.zeros([T,3])
for t in range(1,T):
y[t,0] = mu + eps[t]
y[t,1] = (1-phi_l)*mu + phi_l*y[t-1,1] + eps[t]
y[t,2] = (1-phi_h)*mu + phi_h*y[t-1,2] + eps[t]# Libraries
import pandas as pd
# Convert to DataFrame and plot
df = pd.DataFrame(y)
df.columns = ['White Noise','AR(1) low AC','AR(1) high AC']# libraries
import matplotlib.pyplot as plt
# Plot variables
fig, axs = plt.subplots(len(df.columns),figsize=(6.5,3.5))
for idx, ax in enumerate(axs.flat):
col = df.columns[idx]; y = df[col]
ax.plot(y); ax.set_ylabel(col)
ax.grid(); ax.autoscale(tight=True); ax.label_outer()
print(f'{col}: \
E(y) = {y.mean():.2f}, Std(y) = {y.std():.2f}, \
AC(y) = {y.corr(y.shift(1)):.2f}')White Noise: E(y) = 1.97, Std(y) = 1.02, AC(y) = -0.02
AR(1) low AC: E(y) = 1.94, Std(y) = 1.16, AC(y) = 0.48
AR(1) high AC: E(y) = 1.72, Std(y) = 2.18, AC(y) = 0.88
# Auto-correlation function
from statsmodels.graphics.tsaplots import plot_acf as acf
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
acf(df['AR(1) high AC'],ax)
ax.grid(); ax.autoscale(tight=True);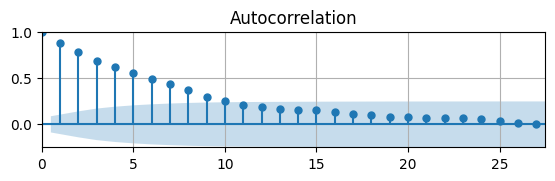
# ARIMA model
from statsmodels.tsa.arima.model import ARIMA
# Define model
mod = ARIMA(df['AR(1) high AC'],order=(1,0,0))
# Estimate model
res = mod.fit()
summary = res.summary()
# Print summary tables
tab0 = summary.tables[0].as_html()
tab1 = summary.tables[1].as_html()
tab2 = summary.tables[2].as_html()
# print(tab0); print(tab1); print(tab2)Estimation Results¶
| Dep. Variable: | AR(1) high AC | No. Observations: | 501 |
|---|---|---|---|
| Model: | ARIMA(1, 0, 0) | Log Likelihood | -718.607 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 1.6774 | 0.390 | 4.302 | 0.000 | 0.913 | 2.442 |
| ar.L1 | 0.8843 | 0.021 | 41.211 | 0.000 | 0.842 | 0.926 |
| sigma2 | 1.0282 | 0.059 | 17.442 | 0.000 | 0.913 | 1.144 |
| Heteroskedasticity (H): | 1.14 | Skew: | -0.15 |
|---|---|---|---|
| Prob(H) (two-sided): | 0.41 | Kurtosis: | 3.45 |
Parameter estimates are close to DGP and significantly different from 0
Residuals have skewness near 0 and kurtosis near 3 so they are probably normally distributed
Modeling UR as AR(1)¶
The U.S. unemployment rate is very persistent.
What if we model it with an AR(1)?
# Libraries
from fredapi import Fred
import pandas as pd
# Read Data
fred_api_key = pd.read_csv('fred_api_key.txt', header=None)
fred = Fred(api_key=fred_api_key.iloc[0,0])
data = fred.get_series('UNRATE').to_frame(name='UR')
data.index = pd.DatetimeIndex(data.UR.index.values,freq=data.UR.index.inferred_freq)
# Plot
fig, ax = plt.subplots(figsize=(6.5,2));
ax.plot(data.UR); ax.set_title('U.S. Unemployment Rate');
ax.yaxis.set_major_formatter('{x:,.1f}%')
ax.grid(); ax.autoscale(tight=True)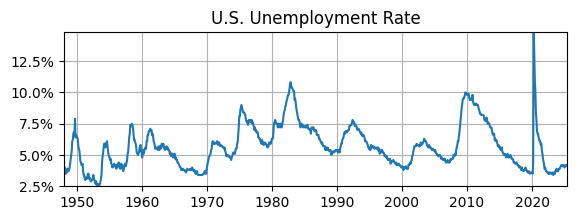
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,2.5))
acf(data.UR,ax);
ax.grid(); ax.autoscale(tight=True)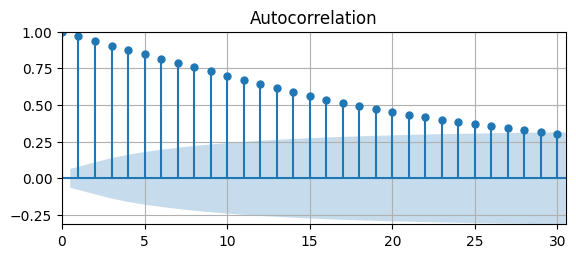
The ACF decays very slow UR might be non-stationary.
Let’s assume it is stationary for a moment and estimate an AR(1) model
# ARIMA model
from statsmodels.tsa.arima.model import ARIMA
# Define model
mod = ARIMA(data.UR,order=(1,0,0))
# Estimate model
res = mod.fit()
summary = res.summary()
# Print summary tables
tab0 = summary.tables[0].as_html()
tab1 = summary.tables[1].as_html()
tab2 = summary.tables[2].as_html()
#print(tab0); print(tab1); print(tab2)Estimation Results¶
| Dep. Variable: | VALUE | No. Observations: | 925 |
|---|---|---|---|
| Model: | ARIMA(1, 0, 0) | Log Likelihood | -496.551 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 5.5470 | 0.761 | 7.289 | 0.000 | 4.055 | 7.039 |
| ar.L1 | 0.9704 | 0.008 | 122.023 | 0.000 | 0.955 | 0.986 |
| sigma2 | 0.1708 | 0.001 | 159.798 | 0.000 | 0.169 | 0.173 |
| Heteroskedasticity (H): | 6.35 | Skew: | 16.87 |
|---|---|---|---|
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 428.90 |
Estimate of AR coeffecient is very high at 0.9704, but the data is not a random walk
Residuals are skewed and have excess kurtosis model is missing nonlinearity
Actual vs. Simulated Data¶
What if we simulated data from AR(1) model setting the parameters to the previous estimates?
What does a simulation from this estimated model look like?
# Assign parameters
T = len(data.UR); mu = 5.547; rho = 0.9704; sigma = np.sqrt(0.1708);
# Draw random numbers
rng = np.random.default_rng(seed=0)
eps = rng.standard_normal(T)
# Simulate time series
URsim = mu*np.ones([T,1])
for t in range(1,T):
URsim[t,0] = (1-rho)*mu + rho*URsim[t-1,0] + sigma*eps[t];# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
acf(URsim,ax)
ax.grid(); ax.autoscale(tight=True);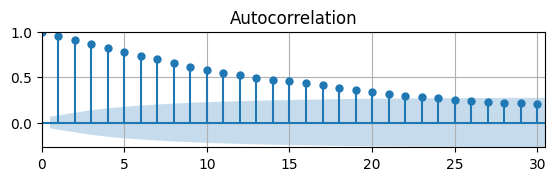
This ACF approaches zero at shorter lags compared to the actual data.
We know an AR(1) model with generates stationary time series.
Maybe the actual UR isn’t stationary?
# Add simulation to DataFrame
data['URsim'] = URsim
# Variables to plot and ylabel
plotme = [['UR','Actual UR'],['URsim','Simulated UR']]
# Plot variables
fig, axs = plt.subplots(len(plotme),figsize=(6.5,3))
for idx, ax in enumerate(axs.flat):
y = data[plotme[idx][0]]; ylabel = plotme[idx][1]
ax.plot(y); ax.set_ylabel(ylabel)
ax.yaxis.set_major_formatter('{x:.0f}%')
ax.grid(); ax.autoscale(tight=True); ax.label_outer()
print(f'{ylabel}: \
E(y) = {y.mean():.2f}, Std(y) = {y.std():.2f}, \
AC(y) = {y.corr(y.shift(1)):.2f}')Actual UR: E(y) = 5.67, Std(y) = 1.71, AC(y) = 0.97
Simulated UR: E(y) = 5.21, Std(y) = 1.34, AC(y) = 0.95
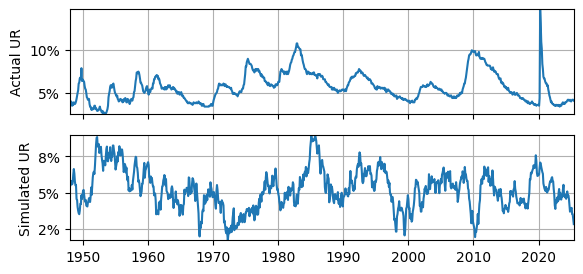
Does it fit?¶
The actual UR is very smooth, but the AR(1) model is not.
The simulated UR often falls below , whereas the actual UR does not.
The actual UR meets or exceeds a few times, whereas the simulated UR does not.
The actual UR rises quickly and falls slowly, whereas the simulated UR seems to rise and fall at roughly the same rates.
This all suggests that the AR(1) model is unable to reproduce some important features of the actual UR.
Partial ACF¶
Most of the slides in this chapter are about the AR(1) model.
Suppose the true DGP is an AR model, but we do not know the order.
When the DGP is a MA model, we can use the ACF to determine the order since it drops off to zero after a certain lag.
But for AR model, the autocorrelation at higher lags is influenced by the intermediate observations between and , and even for an AR(1) model the ACF tapers slowly.
Alternatively, Partial ACF (PACF) helps to identify the order of an AR model.
The PACF at lag is the correlation between and that is not explained by observations in between,
The PACF at lag is denoted as , and plotting against lag forms the PACF plot.
AR(2) Model¶
Let’s simulate the following AR(2) model
where , , , and
We know the DGP and the true order of the AR model. Does the PACF suggest the same order?
# Assign parameters
T = 501; mu = 2; phi_1 = 0.8; phi_2 = 0.15; sigma = 0.5;
# Draw random numbers
rng = np.random.default_rng(seed=0)
eps = rng.standard_normal(T)
# Simulate time series
y = mu*np.ones([T,1])
for t in range(2,T):
y[t,0] = (1-phi_1-phi_2)*mu + phi_1*y[t-1,0] + phi_2*y[t-2,0] + sigma*eps[t]# Convert to DataFrame and plot
df = pd.DataFrame(y)
fig, ax = plt.subplots(figsize=(6.5,2.5))
ax.plot(df); ax.set_title('AR(2) Simulated Data')
ax.grid(); ax.autoscale(tight=True)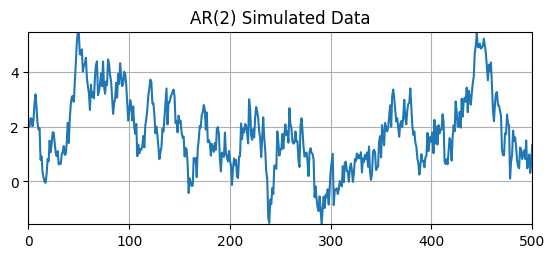
# Partial auto-correlation function
from statsmodels.graphics.tsaplots import plot_pacf as pacf
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
pacf(df,ax)
ax.grid(); ax.autoscale(tight=True);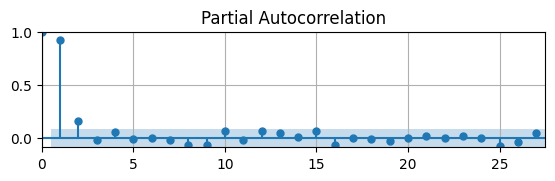
The PACF is significantly different from zero for , which indicates the DGP is probably an AR(2).
So the PACF is good at deterimining order so long as AR coefficients are large enough.
Modeling UR as AR(2)¶
Is a higher order AR model a good fit for the U.S. unemployment rate?
Let’s first plot the PACF of the UR to see if we can determine an order.
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
pacf(data.UR,ax);
ax.grid(); ax.autoscale(tight=True)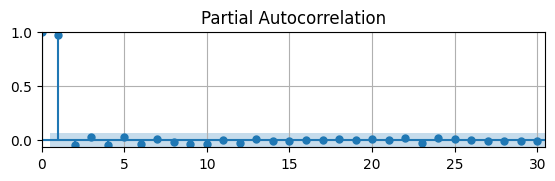
This suggests that an AR(1) might be the best model.
What if we ignore the PACF and estimate an AR(2) anyway?
# Define model
mod = ARIMA(data.UR,order=(2,0,0))
# Estimate model
res = mod.fit()
summary = res.summary()
# Print summary tables
tab0 = summary.tables[0].as_html()
tab1 = summary.tables[1].as_html()
tab2 = summary.tables[2].as_html()
#print(tab0); print(tab1); print(tab2)Estimation Results¶
| Dep. Variable: | VALUE | No. Observations: | 925 |
|---|---|---|---|
| Model: | ARIMA(2, 0, 0) | Log Likelihood | -495.314 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 5.5611 | 0.740 | 7.510 | 0.000 | 4.110 | 7.012 |
| ar.L1 | 1.0208 | 0.009 | 109.007 | 0.000 | 1.002 | 1.039 |
| ar.L2 | -0.0517 | 0.010 | -5.057 | 0.000 | -0.072 | -0.032 |
| sigma2 | 0.1703 | 0.001 | 143.540 | 0.000 | 0.168 | 0.173 |
| Heteroskedasticity (H): | 6.37 | Skew: | 16.65 |
|---|---|---|---|
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 423.48 |
Both AR coefficients are significantly different from 0
But the AR(2) is still linear, i.e., normal and symmetric, so the residuals are still skewed and fat-tailed
PACF did not help to determine that second lag might improve fit
UR First Difference¶
# Year-over-year growth rate
dUR = data.UR.diff(1); dUR = dUR.dropna()
# Plot
fig, ax = plt.subplots(figsize=(6.5,1.5));
ax.plot(dUR); ax.set_title('Change in U.S. Unemployment Rate (month to month)');
ax.yaxis.set_major_formatter('{x:,.0f}pp'); ax.grid(); ax.autoscale(tight=True)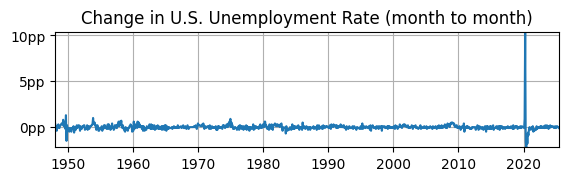
Is it stationary?
Yes, mean looks constant around 0.
Yes, volatility looks constant, except for COVID.
Maybe not, it’s impossible to see if the autocovariance is constant.
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
acf(dUR,ax)
ax.grid(); ax.autoscale(tight=True);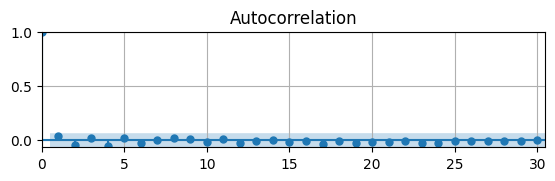
The ACF indicates that the series is probably stationary.
What does the PACF say?
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
pacf(dUR,ax);
ax.grid(); ax.autoscale(tight=True)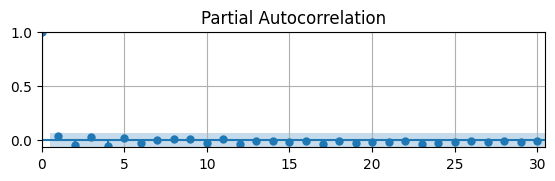
The PACF shows that the autocorrelation is not significantly different from zero for all lags.
What is the best model to estimate? Let’s try MA(1) and AR(1) and compare.
Estimation Results¶
# Define model
mod0 = ARIMA(dUR,order=(0,0,1))
mod1 = ARIMA(dUR,order=(1,0,0))
# Estimate model
res = mod1.fit(); summary = res.summary()
# Print summary tables
tab0 = summary.tables[0].as_html()
tab1 = summary.tables[1].as_html()
tab2 = summary.tables[2].as_html()
#print(tab0); print(tab1); print(tab2)| Dep. Variable: | VALUE | No. Observations: | 924 |
|---|---|---|---|
| Model: | ARIMA(0, 0, 1) | Log Likelihood | -500.699 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.0007 | 0.025 | 0.027 | 0.979 | -0.047 | 0.049 |
| ma.L1 | 0.0398 | 0.008 | 4.893 | 0.000 | 0.024 | 0.056 |
| sigma2 | 0.1731 | 0.001 | 185.366 | 0.000 | 0.171 | 0.175 |
| Heteroskedasticity (H): | 6.54 | Skew: | 16.40 |
|---|---|---|---|
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 419.10 |
The MA coefficient estimate is statistically significantly different from 0.
However, the residuals are still probably heteroskedastic and not normally distributed.
Thus, a linear/normal model is probably not the best choice.
| Dep. Variable: | VALUE | No. Observations: | 924 |
|---|---|---|---|
| Model: | ARIMA(1, 0, 0) | Log Likelihood | -500.757 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.0007 | 0.025 | 0.026 | 0.979 | -0.048 | 0.049 |
| ar.L1 | 0.0363 | 0.008 | 4.344 | 0.000 | 0.020 | 0.053 |
| sigma2 | 0.1731 | 0.001 | 185.413 | 0.000 | 0.171 | 0.175 |
| Heteroskedasticity (H): | 6.55 | Skew: | 16.42 |
|---|---|---|---|
| Prob(H) (two-sided): | 0.00 | Kurtosis: | 419.51 |
The AR coefficient is small/weak but estimate is statistically significantly different from 0.
Like the MA(1) model, the residuals are still probably heteroskedastic and not normally distributed.
This again confirms that a linear/normal model is probably not the best choice.