Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

MA Model

by Professor Throckmorton
for Time Series Econometrics
W&M ECON 408/PUBP 616
Slides

Wold Representation Theorem

  • Wold representation theorem: any covariance stationary series can be expressed as a linear combination of current and past white noise.

    yt=∑i=0∞biεt−iy_t = \sum_{i=0}^\infty b_i \varepsilon_{t-i}
    (1)

  • εt\varepsilon_t is a white noise process with mean 0 and variance σ2\sigma^2.

  • b0=1b_0 = 1, and ∣∑i=0∞bi∣<∞|\sum_{i=0}^\infty b_i | < \infty, which ensures the process is stable.

  • εt\varepsilon_t, a.k.a. an innovation, represents new information that cannot be predicted using past values.

Key aspects

  • Generality: The Wold Representation is a general model that can represent any covariance stationary time series. This is why it is important for forecasting.

  • Linearity: The representation is a linear function of its innovations or “general linear process”.

  • Zero Mean: The theorem applies to zero-mean processes, but this is without loss of generality because any covariance stationary series can be expressed in deviations from its mean, yt−μy_t-\mu.

  • Innovations: The Wold representation expresses a time series in terms of its current and past shocks/innovations.

  • Approximation: In practice, because an infinite distributed lag isn’t directly usable, models like moving average (MA), autoregressive (AR), and autoregressive moving average (ARMA) models are used to approximate the Wold representation.

MA Model

  • The moving average (MA) model expresses the current value of a series as a function of current and lagged unobservable shocks (or innovations)

  • The MA model of order qq, denoted as MA(qq), is defined as:

    yt=μ+εt+θ1εt−1+θ2εt−2+...+θqεt−qy_t = \mu + \varepsilon_t + \theta_1 \varepsilon_{t−1} + \theta_2 \varepsilon_{t−2} + ... + \theta_q \varepsilon_{t−q}
    (2)

    • μ\mu is the mean or intercept of the series.

    • εt\varepsilon_t is a white noise process with mean 0 and variance σ2\sigma^2.

    • θ1,θ2,…,θq\theta_1,\theta_2,\ldots,\theta_q are the parameters of the model.

Key aspects

  • Stationarity: MA models are always stationary.

  • Approximation: Finite-order MA processes are a natural approximation to the Wold representation, which is MA(∞\infty).

  • Autocorrelation: The ACF of an MA(qq) model cuts off after lag qq, i.e., the autocorrelations are zero beyond displacement qq. This is helpful in identifying a suitable MA model for time series data.

  • Forecasting: MA models are not forecastable more than qq steps ahead, apart from the unconditional mean, μ\mu.

  • Invertibility: An MA model is invertible if it can be expressed as an autoregressive model with an infinite number of lags.

Unconditional Moments

  • The variance of an MA process depends on the order of the process and the variance of the white noise, εt∼i.i.d.N(0,σ2)\varepsilon_t \overset{i.i.d.}{\sim} N(0,\sigma^2)

  • MA(1) Process: yt=μ+εt+θεt−1y_t = \mu + \varepsilon_t + \theta\varepsilon_{t-1}

    • E(yt)=μ+E(εt)+θE(εt−1)=μE(y_t) = \mu + E(\varepsilon_t) + \theta E(\varepsilon_{t-1}) = \mu

    • Var(yt)=Var(εt)+θ2Var(εt−1)=σ2(1+θ2)Var(y_t) = Var(\varepsilon_t) + \theta^2 Var(\varepsilon_{t-1}) = \sigma^2(1 + \theta^2)

    • Std(yt)=σ2(1+θ2)Std(y_t) = \sqrt{\sigma^2(1 + \theta^2)}

  • MA(qq) Process: yt=μ+εt+θ1εt−1+⋯+θqεt−qy_t = \mu + \varepsilon_t + \theta_1\varepsilon_{t-1} + \dots + \theta_q\varepsilon_{t-q}

    • E(yt)=μE(y_t) = \mu

    • Var(yt)=σ2(1+θ12+⋯+θq2)Var(y_t) = \sigma^2(1 + \theta_1^2 + \dots + \theta_q^2)

    • Std(yt)=Var(yt)Std(y_t) = \sqrt{Var(y_t)}

Autocorrelation Function

  • MA(1) Process: yt=μ+εt+θεt−1y_t = \mu + \varepsilon_t + \theta\varepsilon_{t-1}

    • γ(0)=E[(yt−μ)(yt−μ)]=Var(yt)=σ2(1+θ2)\gamma(0) = E[(y_t-\mu)(y_t-\mu)] = Var(y_t) = \sigma^2(1 + \theta^2)

    • γ(1)=E[(yt−μ)(yt−1−μ)]\gamma(1) = E[(y_t-\mu)(y_{t-1}-\mu)]

    =E[(εt+θεt−1)(εt−1+θεt−2)]=E[εtεt−1+εtθεt−2+θεt−1εt−1+θεt−1θεt−2]=θE[εt−12]=θVar[εt−1]=θσ2\begin{align*} &= E[(\varepsilon_t + \theta\varepsilon_{t-1})(\varepsilon_{t-1} + \theta\varepsilon_{t-2})] \\ &= E[\varepsilon_t\varepsilon_{t-1} + \varepsilon_t\theta\varepsilon_{t-2} + \theta\varepsilon_{t-1}\varepsilon_{t-1} + \theta\varepsilon_{t-1}\theta\varepsilon_{t-2}] \\ &= \theta E[\varepsilon_{t-1}^2] = \theta Var[\varepsilon_{t-1}] \\ &= \theta\sigma^2 \end{align*}
    (3)

    • γ(τ)=0\gamma(\tau) = 0 for ∣τ∣>1|\tau| > 1

    • ρ(0)=1\rho(0) = 1, i.e., any series is perfectly correlated with itself

    • ρ(1)=γ(1)/γ(0)=θ/(1+θ2)\rho(1) = \gamma(1)/\gamma(0) = \theta/(1 + \theta^2)

    • ρ(τ)=0\rho(\tau) = 0 for ∣τ∣>1|\tau| > 1

  • MA(qq) process: yt=εt+θ1εt−1+⋯+θqεt−qy_t = \varepsilon_t + \theta_1\varepsilon_{t-1} + \dots + \theta_q\varepsilon_{t-q}

    • ρ(0)=1\rho(0) = 1

    • ρ(k)=θk+∑i=1q−kθiθi+k1+∑i=1qθi2\rho(k) = \frac{\theta_k + \sum_{i=1}^{q-k} \theta_i\theta_{i+k}}{1 + \sum_{i=1}^{q} \theta_i^2} for 1≤k≤q1 \le k \le q

    • ρ(τ)=0\rho(\tau) = 0 for ∣τ∣>q|\tau| > q

MA Model as DGP

Let’s compare a couple different MA models to their underlying white noise.

  1. White noise:

yt=μ+εty_t = \mu + \varepsilon_t
(4)

  1. MA(1):

yt=μ+εt+θ1εt−1y_t = \mu + \varepsilon_t + \theta_1 \varepsilon_{t−1}
(5)

  1. MA(3):

yt=μ+εt+θ1εt−1+θ2εt−2+θ3εt−3y_t = \mu + \varepsilon_t + \theta_1 \varepsilon_{t−1} + \theta_2 \varepsilon_{t−2} + \theta_3 \varepsilon_{t−3}
(6)
# Import libraries
#   Plotting
import matplotlib.pyplot as plt
#   Scientific computing
import numpy as np
#   Data analysis
import pandas as pd

DIY simulation

# Assign parameters
T = 501; mu = 2; theta1 = 0.6; theta2 = 0.5; theta3 = 0.7;
# Draw random numbers
rng = np.random.default_rng(seed=0)
eps = rng.standard_normal(T)
# Simulate time series
y = np.zeros([T,3])
for t in range(3,T):
    y[t,0] = mu + eps[t]
    y[t,1] = mu + eps[t] + theta1*eps[t-1]
    y[t,2] = (mu + eps[t] + theta1*eps[t-1] 
               + theta2*eps[t-2] + theta3*eps[t-3])
# Convert to DataFrame and plot
df = pd.DataFrame(y)
df.columns = ['White Noise','MA(1)','MA(3)']
df.plot(subplots=True,grid=True)
array([<Axes: >, <Axes: >, <Axes: >], dtype=object)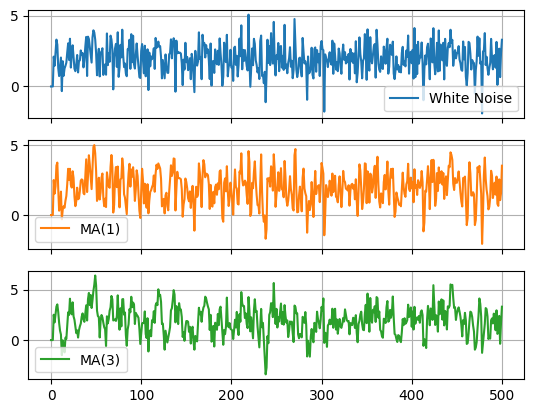
<Figure size 640x480 with 3 Axes>
# Plot variables
fig, axs = plt.subplots(len(df.columns),figsize=(6.5,3.5))
for idx, ax in enumerate(axs.flat):
    col = df.columns[idx]
    y = df[col]
    ax.plot(y); ax.set_ylabel(col)
    ax.grid(); ax.autoscale(tight=True); ax.label_outer()
    print(f'{col}: \
E(y) = {y.mean():.2f}, \
Std(y) = {y.std():.2f}, \
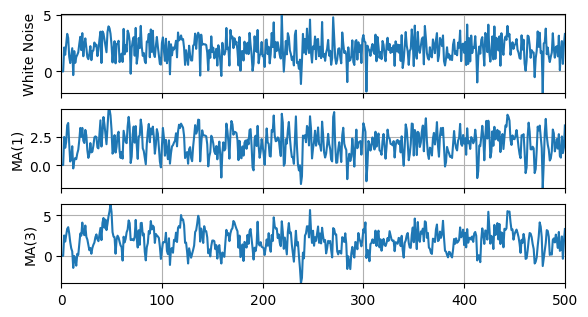
AC(y) = {y.corr(y.shift(1)):.2f}')
White Noise: E(y) = 0.06, Std(y) = 0.97, AC(y) = -0.05
MA(1): E(y) = 0.02, Std(y) = 1.18, AC(y) = 0.46
MA(3): E(y) = -0.17, Std(y) = 1.33, AC(y) = 0.57
<Figure size 650x350 with 3 Axes>

Using statsmodels

#   ARIMA Process
from statsmodels.tsa.arima_process import ArmaProcess as arma

# Set rng seed
rng = np.random.default_rng(seed=0)
# Create models (coefficients include zero lag)
wn = arma(ma=[1]);
ma1 = arma(ma=[1,theta1])
ma3 = arma(ma=[1,theta1,theta2,theta3])
# Simulate models
y = np.zeros([T,3])
y[:,0] = wn.generate_sample(T)
y[:,1] = ma1.generate_sample(T)
y[:,2] = ma3.generate_sample(T)
# Convert to DataFrame
df = pd.DataFrame(y)
df.columns = ['White Noise','MA(1)','MA(3)']
df.plot(subplots=True,grid=True)
array([<Axes: >, <Axes: >, <Axes: >], dtype=object)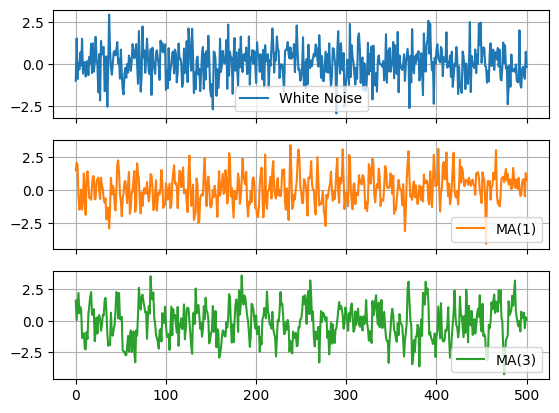
<Figure size 640x480 with 3 Axes>
# Auto-correlation function
from statsmodels.graphics.tsaplots import plot_acf as acf
# Plot Autocorrelation Function
fig, ax = plt.subplots(figsize=(6.5,1.5))
acf(df['MA(3)'],ax)
ax.grid(); ax.autoscale(tight=True);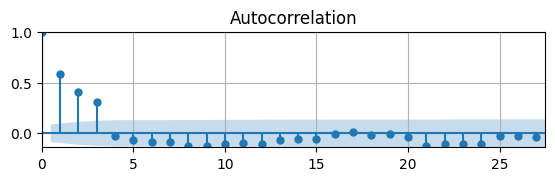
<Figure size 650x150 with 1 Axes>

Since the DGDP is an MA(3), the ACF shows the correlations are only significant for the first 3 lags.

Estimating MA Model

  • In an MA model, the current value is expressed as a function of current and lagged unobservable shocks.

    • However, the error terms are not observed directly and must be inferred from the data and estimated parameters.

    • This creates a nonlinear relationship between the data and the model’s parameters.

  • The statsmodels module has a way to define an MA model and estimate its parameters.

  • The general model is Autoregressive Integrated Moving Average Model, or ARIMA(p,d,qp,d,q), of which MA(qq) is a special case.

  • The argument order=(p,d,q) specifies the order for the autoregressive, integrated, and moving average components.

  • See statsmodels for more information.

# ARIMA model
from statsmodels.tsa.arima.model import ARIMA
# Define model
mod = ARIMA(df['MA(3)'],order=(0,0,3))
# Estimate model
res = mod.fit()
summary = res.summary()
# Print summary tables
tab0 = summary.tables[0].as_html()
tab1 = summary.tables[1].as_html()
tab2 = summary.tables[2].as_html()
# print(tab0); print(tab1); print(tab2)
Dep. Variable:MA(3)No. Observations:501
Model:ARIMA(0, 0, 3)Log Likelihood-700.202
Date:Wed, 05 Feb 2025AIC1410.405
Time:14:24:16BIC1431.488
Sample:0-501HQIC1418.677
coefstd errzP>|z|[0.0250.975]
const-0.13910.125-1.1140.265-0.3840.106
ma.L10.61990.03318.7130.0000.5550.685
ma.L20.52480.03714.2510.0000.4530.597
ma.L30.69490.03420.1580.0000.6270.762
sigma20.95400.06414.8190.0000.8281.080
Ljung-Box (L1) (Q):0.09Jarque-Bera (JB):1.32
Prob(Q):0.76Prob(JB):0.52
Heteroskedasticity (H):1.08Skew:0.08
Prob(H) (two-sided):0.61Kurtosis:2.80

Invertibility of MA(1)

  • Suppose yt=εt+θεt−1y_t = \varepsilon_t + \theta \varepsilon_{t−1} and ∣θ∣<1|\theta| < 1.

  • Rearrange to get εt=yt−θεt−1\varepsilon_t = y_t - \theta \varepsilon_{t−1}, which holds at all points in time, e.g.,

    εt−1=yt−1−θεt−2εt−2=yt−2−θεt−3\begin{align*} \varepsilon_{t-1} &= y_{t-1} - \theta \varepsilon_{t−2} \\ \varepsilon_{t-2} &= y_{t-2} - \theta \varepsilon_{t−3} \end{align*}
    (7)

  • Combine these (i.e., recursively substitute) to get an AR(∞)AR(\infty) Model

    εt=yt−θyt−1−θ2yt−2−θ3yt−3−⋯=yt−∑j=1∞θjyt−j\varepsilon_t = y_t - \theta y_{t-1} - \theta^2 y_{t-2} - \theta^3 y_{t-3} - \cdots = y_t - \sum_{j=1}^\infty \theta^j y_{t-j}
    (8)

    or

    yt=∑j=1∞θjyt−j+εty_t = \sum_{j=1}^\infty \theta^j y_{t-j} + \varepsilon_t
    (9)

  • The innovation, εt\varepsilon_t (something unobservable), can be “inversely” expressed by the data, but that’s only possible if ∣θ∣<1|\theta| < 1.

Part 1
Stationarity
Part 2
AR Model